When an electromagnetic wave encounters a boundary between two dielectric media, part of the wave is reflected and part is transmitted. Due to energy conservation, the total power carried by the incident wave must equal the sum of the powers carried by the reflected and transmitted waves, assuming there is no absorption. Additionally, Maxwell’s equations require that the tangential components of the electric and magnetic fields remain continuous across the boundary. To describe this behavior quantitatively, I derive the Fresnel equations for s-polarized (transverse electric, TE) light, where the electric field is perpendicular to the plane of incidence.

Deriving the Fresnel Equations for Isotropic Case

The figure below shows the geometry of the problem. A wave is incident from medium 1 (left) with refractive index $n_1$, hitting an interface with medium 2 (right) with refractive index $n_2$. The electric field vectors $\mathbf{E}_i, \mathbf{E}_r, \mathbf{E}_t$ are all perpendicular to the plane of incidence (s-polarized), while the corresponding magnetic fields $\mathbf{H}_i, \mathbf{H}_r, \mathbf{H}_t$ lie in the plane.

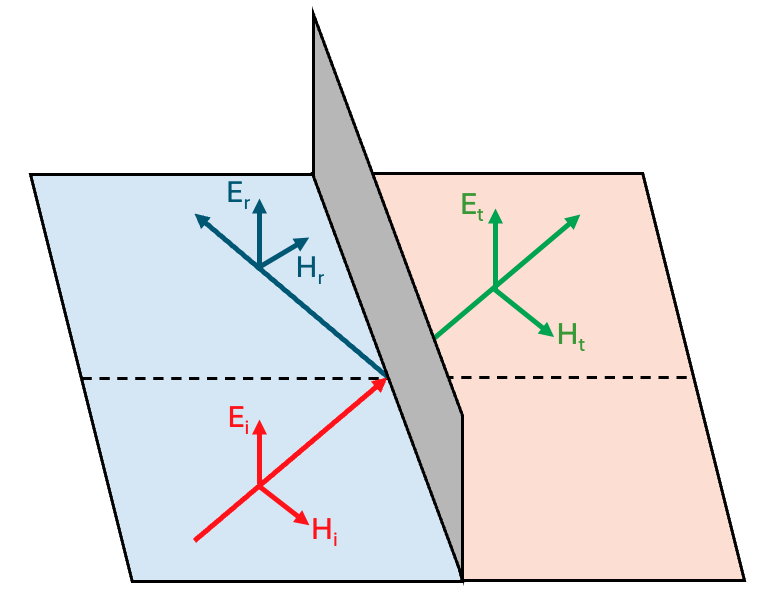
Note: The direction of $\mathbf{E}$ does not change upon reflection or transmission. However, the direction of $\mathbf{H}$ does flip for the reflected wave. This preserves the right-hand rule: since the wave vector $\mathbf{k}$ reverses in the reflected case, and $\mathbf{E}$ is fixed, the magnetic field $\mathbf{H}$ must also flip direction to remain orthogonal and maintain $\mathbf{k} = \mathbf{E} \times \mathbf{H}$.

In the absence of free charges or currents, Maxwell’s equations reduce to:

From these, we derive the following boundary conditions at the planar interface:

• Continuity of tangential $\mathbf{E}$: \(E_i + E_r = E_t\)
• Continuity of tangential $\mathbf{H}$: \(H_i \cos \theta_i - H_r \cos \theta_r = H_t \cos \theta_t\)

For s-polarized light, we relate electric and magnetic fields via the intrinsic impedance of the medium:

Substituting into the boundary conditions:

1. Electric field continuity: \(E_i + E_r = E_t\)

2. Magnetic field continuity: \(\frac{E_i - E_r}{\eta_1} \cos \theta_i = \frac{E_t}{\eta_2} \cos \theta_t\)

This system can be solved algebraically to obtain the Fresnel coefficients for s-polarized light.

Fresnel Equations (s-Polarization)

Let’s define the reflection and transmission coefficients:

• Reflection coefficient: \(r_s = \frac{n_1 \cos \theta_i - n_2 \cos \theta_t}{n_1 \cos \theta_i + n_2 \cos \theta_t}\)
• Transmission coefficient: \(t_s = \frac{2 n_1 \cos \theta_i}{n_1 \cos \theta_i + n_2 \cos \theta_t}\)

These describe the amplitude ratios of reflected and transmitted electric fields relative to the incident field. The reflection and transmission coefficients describe how field amplitudes are split at the interface.

Note: These coefficients apply to plane waves under the assumption of linear, isotropic, lossless dielectrics. The derivation assumes monochromatic, time-harmonic waves and neglects any surface roughness or absorption.

Power and Energy Conservation

The coefficients $r_s$ and $t_s$ describe field amplitudes. To compute power reflectance and transmittance:

• Reflectance (fraction of incident power reflected): \(R_s = |r_s|^2\)
• Transmittance (fraction of incident power transmitted): \(T_s = \frac{n_2 \cos \theta_t}{n_1 \cos \theta_i} |t_s|^2\)

The factor $\frac{n_2 \cos \theta_t}{n_1 \cos \theta_i}$ accounts for the change in wave impedance and geometry across the interface. From energy conservation:

This condition verifies that no energy is lost at the boundary (i.e., no absorption or gain). Power is split and must sum up to unity in the lossless case.

In a future post, I will go over how Snell’s Law follows from phase matching conditions.